clubpro

Background

clubpro is an implementation of a subset of the methods described in Grice (2011) for classification of observations using binary procrustes rotation. Binary procrustes rotation can be used to quantify how well observed data can be classified into known categories. A high degree of classification accuracy indicates that the ordering of the observed data is well explained by particular categories or experimental conditions.

Set up

clubpro can be installed from CRAN with the command install.packages("clubpro") and loaded in the usual way.

library(clubpro)

The plots provided by clubpro use the colour palette loaded in the current R session. You may specify the plot colours by passing a vector of colours to palette().

palette(c("#0073C2", "#EFC000", "#868686"))

Classifying catch location by jellyfish size

Hand et. at. (1994) provide data on the width and length in mm of jellyfish caught at two locations in New South Wales, Australia: Dangar Island and Salamander Bay.

To quantify how well jellyfish width is predicted by catch location, binary procrustes rotation can be performed with clubpro by passing a formula object of the form observed variable ~ predictor variables(s) and a data.frame containing the data to the club() function.

mod <- club(width ~ location, data = jellyfish)

The two most important statistics returned by the club() function are the percentage of correct classifications (PCC), and the chance-value.

The PCC is the percenatge of observations in the data which are classified into the correct category. The PCC returned by club() can be accessed using the pcc() function.

pcc(mod)
#> [1] 84.78261

The chance-value is computed using a randomisation test to determine how frequently a PCC at least as high as that computed for the observed ordering of data is found from random reorderings of the data. Calling the cval() function on an object returned by club() shows the chance-value of the model. Note that because the chance-value is computed using a randomisation test, the value will be slightly different each time the model is run.

cval(mod)
#> [1] 0.011

More detailed classification model results can be returned using the summary() function. Note that values in the summary output are rounded according to the digits argument to summary which defaults to 2.

summary(mod)
#> ********** Model Summary **********
#> 
#> ----- Classification Results -----
#> Observations:  46 
#> Missing observations:  0 
#> Target groups:  2 
#> Correctly classified observations:  39 
#> Incorrectly classified observations:  7 
#> Ambiguously classified observations:  0 
#> PCC:  84.78 
#> Median classification strength index:  1 
#> 
#> ----- Randomisation Test Results -----
#> Random reorderings:  1000 
#> Minimum random PCC:  52.17 
#> Maximum random PCC:  86.96 
#> Chance-value:  0.01

The classification of the observed data can be visualised by plotting the model object using the plot() function.

plot(mod)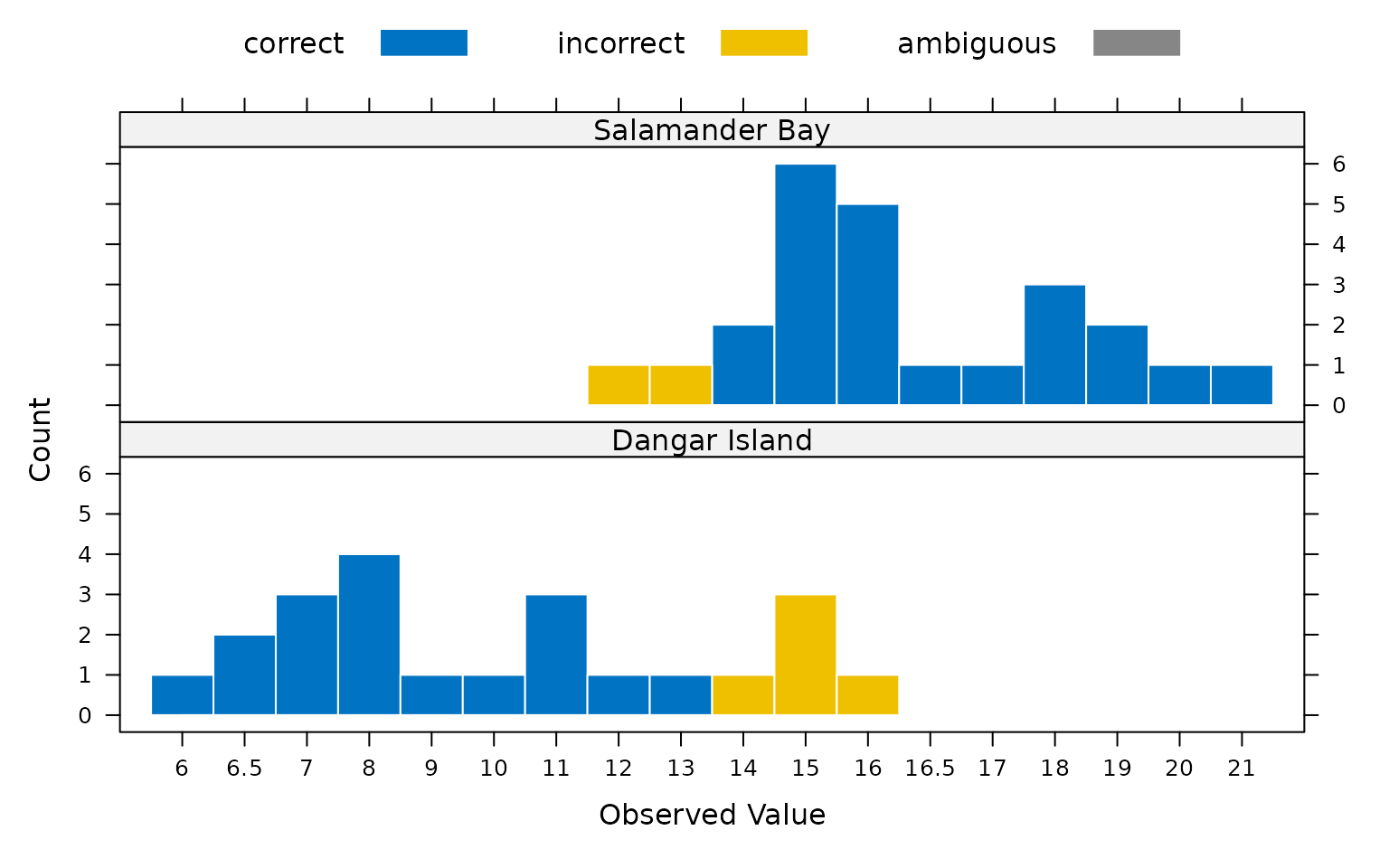

Plotting the classification results shows that observed width values of 11 mm and smaller are consistently placed into the Dangar Island category, while observed width values of at least 16.5 mm are all placed into the Salamader Bay category. From these results we can see that the boundary between the two categories is somewhere between 11 and 16.5. However, it is not clear from the plot exactly where the most likely boundary falls. Grice et. al. (2016) suggest that in the case of binary clasification, the optimal category boundary can be determined by calculating a PCC for each possible boundary location. This can be achieved using the threshold() function.

threshold(mod)
#>     obs      PCC
#> 1   6.0 54.34783
#> 2   6.5 58.69565
#> 3   7.0 65.21739
#> 4   8.0 73.91304
#> 5   9.0 76.08696
#> 6  10.0 78.26087
#> 7  11.0 84.78261
#> 8  12.0 84.78261
#> 9  13.0 84.78261
#> 10 14.0 82.60870
#> 11 15.0 76.08696
#> 12 16.0 67.39130
#> 13 16.5 65.21739
#> 14 17.0 63.04348
#> 15 18.0 56.52174
#> 16 19.0 52.17391
#> 17 20.0 50.00000

Plotting the object returned by threshold() shows that three adjacent category boundary locations produce equal maximum PCCs. This indicates that the optimal category boundary for classification occurs between 11 and 13 mm.

plot(threshold(mod))

For each observation, a classification strength index (CSI) between 0 and 1 is returned. A value of 1 indicates that an observed value was matched perfectly by the rotation, whereas lower CSI values indicate that observations were matched less well. The CSI values can be accessed using the csi() function, or visualised by plotting the object returned by a call to the csi() function.

mod_csi <- csi(mod)
plot(mod_csi)

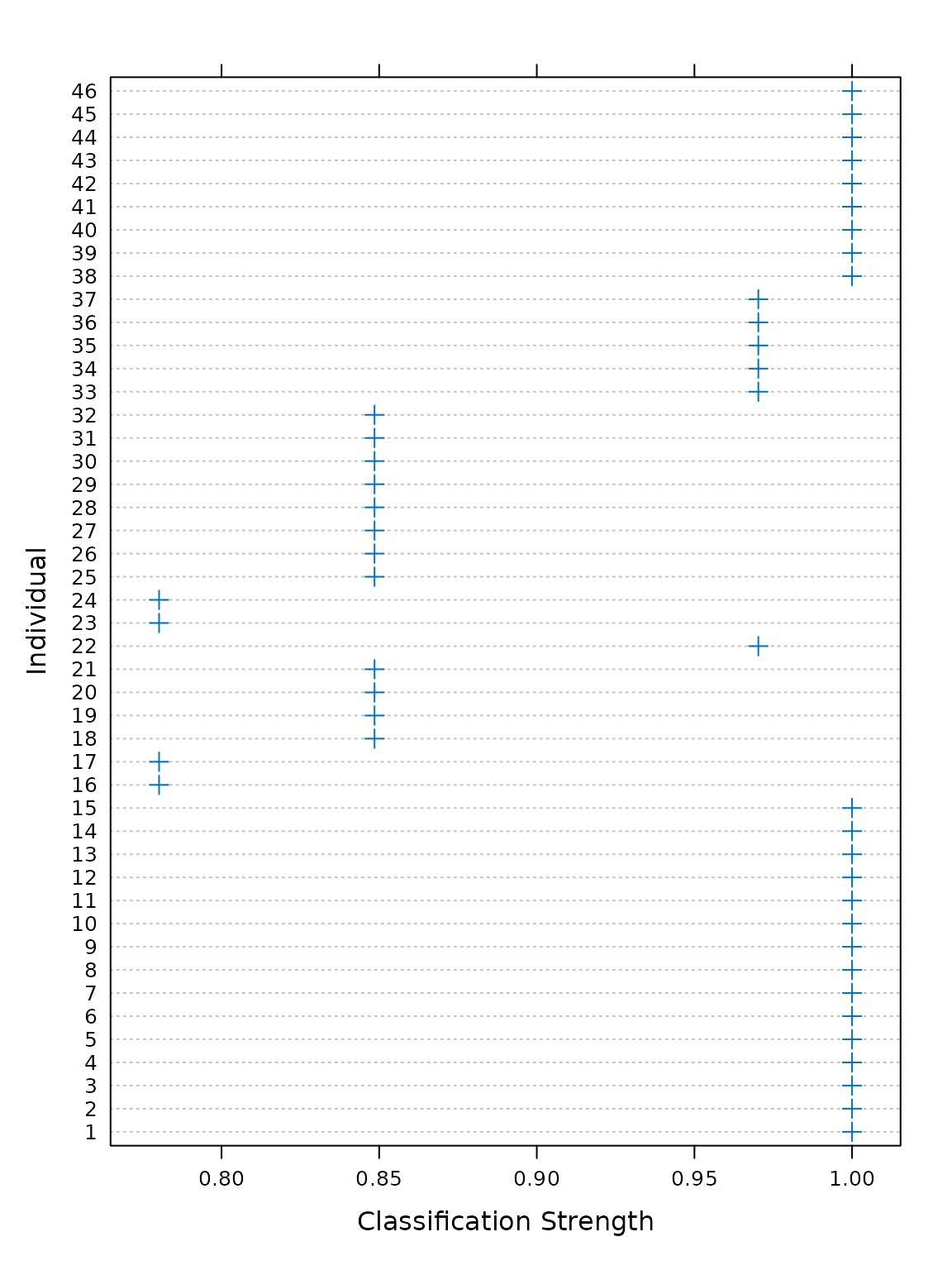
The predicted categories determined by the model can be tabulated using the predict() function. In this case, of the 22 jellyfish caught at Dangar Island, 17 were classified as having come from Dangar Island and 5 were classified as having come from Salamander Bay. Of the 24 jellyfish caught at Salamander Bay, 2 were classified as having come from Dangar Island and 22 were correctly classified as having come from Salamander Bay.

predict(mod)
#>                 
#>                  Dangar Island Salamander Bay
#>   Dangar Island             17              5
#>   Salamander Bay             2             22

These predictions can be visualised as a mosaic plot by plotting the object returned by the predict() function.

plot(predict(mod))

The same information can be tabulated in terms of prediction accuracy using the accuracy() function.

accuracy(mod)
#>                 
#>                  correct incorrect ambiguous
#>   Dangar Island       17         5         0
#>   Salamander Bay      22         2         0

As with predicted categories, prediction accuracy can also be plotted in the form of a mosaic plot using plot(accuracy()).

plot(accuracy(mod))

The calculation of the chance-value as the frequency of occurance PCCs from randomly reordered data at least as high as the PCC of the observed data ordering can be visualised by plotting the output of the pcc_replicates() function. Calling the plot() function on the output of pcc_replicates() produces a histogram of the PCCs resulting from all random orderings of the data. The chance value calculated by the model is the frequency with which PCCs produced from random reorderings of the data are at least as high as the PCC produced by the observed data ordering, indicated in the plot by a dashed vertical line.

plot(pcc_replicates(mod))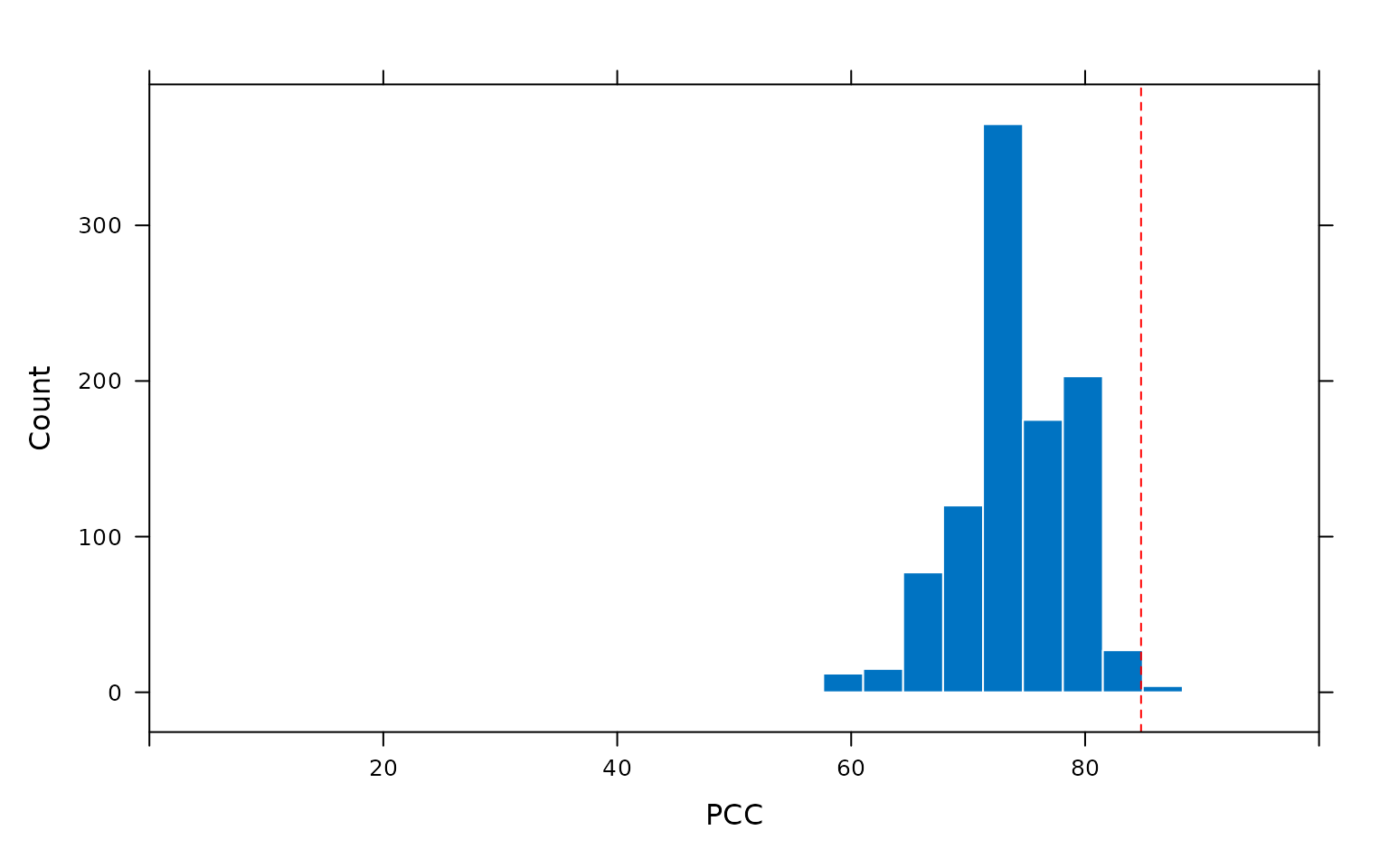

References

Grice, J. W. (2011). Observation oriented modeling: Analysis of cause in the behavioral sciences. Academic Press.

Grice, J. W., Cota, L. D., Barrett, P. T., Wuensch, K. L., & Poteat, G. M. (2016). A Simple and Transparent Alternative to Logistic Regression. Advances in Social Sciences Research Journal, 3(7), 147–165.

Hand, D. J., Daly, F., Lunn, A. D., McConway, K. J. and Ostrowski, E. (1994). A Handbook of Small Data Sets. Chapman & Hall.